Tema 4: Afinidad y homología
Una afinidad es una correspondencia entre elementos, de manera que a cada punto le hacemos corresponder un punto, a cada recta, una recta y, en general, a cada figura plana, otra figura plana.
Los elementos que intervienen en la afinidad son:
- El eje de afinidad
- Un par de puntos afines
Lo más importante, para evitar confundirlo con la Homología, es que la Afinidad se caracteriza por una dirección, es decir, que los puntos afines se encuentran sobre rectas paralelas unas a otras. Se puede entender que en la Afinidad, el vértice se encuentra en el infinito y, por ello, se le considera un caso particular de Homología.
El caballo de batalla
El ejercicio más sencillo que se te puede presentar en afinidad tendrá el siguiente aspecto:
Dados:
- Un eje de afinidad
- Un punto y su afín
- Una figura plana
Se pide:
- Determinar la figura afín de la dada.
Pongamos el ejemplo de un cuadrilátero.
Como ves, en el enunciado partes de un cuadrilátero, un punto con su afín (A-A’) y un Eje de afinidad. A continuación explico la resolución del ejercicio.
Dirección de la afinidad
La dirección de la homología viene definida al unir el punto A con el A’. Ya sabemos que los homólogos de los puntos dados se encontrarán en rectas paralelas a esta. Podemos por lo tanto trazar rectas paralelas a A-A’ pasando por los puntos B, C y D.
Obtener nuevos puntos afines
Puesto que ya conocemos el punto afín de A, lo utilizaremos como base para obtener los demás. Unimos A con B y lo prolongamos hasta el eje. Desde ahí, unimos con el homólogo A’ y también lo prolongamos, de manera que corta a la recta de la dirección de afinidad que pasa por B. Obtenemos así B’.
Para obtener el punto afín D’ seguimos el mismo proceso: unimos A con D y lo prolongamos hasta el Eje. Desde ahí unimos con el punto afín A’. D’ se encontrará en el corte con la recta paralela a la dirección de afinidad que pasa por D.
Una vez que hemos obtenido nuevos puntos afines (B’ y D’) podemos utilizarlos como base para resolver los que nos quedan. Yo he obtenido C’apoyándome en D, pero fíjate que también sería posible definirlo a través deB.
Los 3 trucos de la afinidad que te prometí
Fíjate en el ejercicio anterior. Observa que la recta A’-B’ es afín en toda su longitud a la recta A-B. ¿Qué quiere decir eso? Que cualquier punto que dibujes sobre la recta A-B tendrá su punto afín sobre la recta A’-B’. Basta con dibujar una recta paralela a la dirección de afinidad por dicho punto y ¡listo!
¿Qué pasa en el punto de corte de ambas rectas? Date cuenta de que ambas rectas se cortan en el Eje. No es casual.
¡Atento! porque viene el secreto
Truco nº 1
Cualquier punto que se encuentre en el Eje, tiene su afín en sí mismo.
Lo aplicamos en el siguiente ejemplo:
En este emplo vemos que los puntos C y D se encuentran sobre el Eje. Eso quiere decir que tendrán sus afines en el mismo eje. No tenemos que hacer nada, ¡ya están ahí!
Y para obtener esos puntos nos da exactamente igual dónde esté el punto afín de A, no influye para nada.
Truco nº 2
Cuando una recta sea paralela al Eje, su recta afín también será paralela al Eje. Sencillo pero brillante.
Te explico por qué ocurre esto: cualquier recta debe encontrar su afín y todas tienen un punto común sobre el Eje. La singularidad de las rectas paralelas al Eje es que dicho punto se encuentra en el infinito, puesto que realmente no tienen punto de corte con el Eje. Por tanto, es sencillo entender que tanto la recta original como la afín tengan su punto de corte en el infinito, o, lo que es lo mismo, que sean paralelas al Eje.
Por tanto, si en el ejercicio teníamos que el lado A-B es paralelo al Eje y ya nos habían dado como enunciado el punto afín A’, sólo tenemos que trazar una recta paralela al Eje que pase por A’ para obtener B’. Por supuesto, B’estará sobre una recta paralela a la dirección de afinidad, que quedó definida por A-A’.
Truco nº3
El último truco tiene que ver con la circunferencia.
Ahí va: divide la circunferencia en 8 partes de manera que uno de los diámetros que utilices sea paralelo al Eje de Afinidad. Otro será perpendicular al primero y los otros dos diámetros formarán 45º. Esto te hará la vida infinitamente más sencilla. Tendrás que dibujar menos líneas y, por tanto:
- Ahorrarás tiempo
- Tu dibujo será más preciso
Como he dicho antes, cualquier recta paralela al Eje tiene otra recta paralela al Eje como afín. Es por ello que de esta manera sólo tendrás que encontrar 5 puntos afines.
Sólo he tenido que encontrar la recta afín de 1-5 (que pasa por el centro O y es perpendicular al Eje), así como de 4-8 (que forma 45º). El resto de puntos afines se obtendrán trazando paralelas al Eje por los puntos 4′, 8′ y O’.
Fácil, ¿no?
Ejercicio tipo Prueba de Acceso a la Universidad
Bueno, hasta aquí la teoría. Vamos a aplicarlo a un ejercicio típico de las PAU. Aunque el ejercicio está resuelto más abajo, te dejo las coordenadas precisas de cada punto por si quieres hacerlo en casa. Las coordenadas están dadas en centímetros y referenciadas a la esquina inferior izquierda de un folio tamaño DIN-A4.
– Dados los puntos A (18.3, 24.1), O (22.1, 19.7) y P (18.1, 11.1) junto con sus afines A’ (16.5, 3), O’ (9.2, 11.3) y P’ (18.1, 11.1),
– Se pide:
- Dibujar el Eje de afinidad que definen
- Dibujar el hexágono inscrito en una circunferencia de radio 4.7cm, sabiendo que tiene su centro en O’ y que dos de sus vértices se encuentran en la recta A’-O’.
- Dibujar el hexágono afín.
El eje de afinidad
En primer lugar definimos el Eje de afinidad. Con los datos que contamos, podemos saber que el punto P-P’ pertenece al Eje, puesto que, por definición, cuando un punto y su homólogo coinciden, significa que dicho punto se encuentra en el Eje.
Por otro lado tenemos definidos dos puntos y sus afines. Las rectas que unen dichos puntos serán también afines. Como hemos visto anteriormente, donde se corten dichas rectas definirá otro punto del Eje. Por tanto, unimos A con Oy A’ con O’ y los prolongamos hasta que se corten.
Al unir el punto de intersección con P≡P’ obtenemos el Eje de afinidad. Sencillo, ¿no? Pues esto suele valer 1 punto en las PAU.
El hexágono
Ahora sabemos que, centrado en O’, tenemos que dibujar un hexágono de radio 4.7cm. y que dos de sus vértices se encuentran sobre la recta A’-O’.
Pues nada más fácil. Pinchamos con el compás en O’ y trazamos una circunferencia con el mencionado radio. Eso nos define dos puntos de corte con la recta A’-O’, que serán vértices del hexágono final y que llamaremos 2’y 5’.
Puesto que sabemos que el radio del hexágono es igual al lado, trazamos dos arcos de circunferencia, uno con centro en 2’ y el otro en 5’, ambos con radio 4.7cm y estos nos definirán los otros cuatro vértices del hexágono: 1’, 3’, 4’ y 6’.
– ¡Buah! ¿Otro punto consigo con esto?
– ¡Sí! Normalmente sí, incluso 1.5, depende del año.
El hexágono afín
La dirección de afinidad la tenemos ya definida por las rectas A-A’ o, lo que es lo mismo, su paralela O-O’. Los puntos afines a cada uno de los vértices del hexágono se encontrarán en rectas paralelas a esta dirección que pasen por cada punto. Así que eso ya podemos trazarlo.
Puesto que 2’ y 5’ se encentran sobre la recta A’-O’, sus puntos afines 2 y 5se encontrarán sobre la recta A-O, que ya tenemos dibujada.
Para el punto afín de 1’, lo unimos con otro punto del que ya conozcamos su afín. Lo más sencillo será utilizar el centro O’, porque simultáneamente estamos obteniendo el afín del punto 4’. Prolongamos esa recta hasta el Eje de afinidad y la unimos con el punto O. Así obtendremos los puntos afines 1 y4.
El punto 6 se obtiene de la misma manera, uniendo 6’ con O’, llevando la recta hasta el Eje y luego uniendo con O.
¿Y el punto 3?
El punto quizá más complicado es el 3’, porque se encuentra al otro lado del Eje de Afinidad y puede resultarnos más confuso. En realidad 3’ pertenece a la recta O’-6’, cuya recta afín ya tenemos: O-6. Sólo habría que prolongar dicha recta O-6 hasta que corte a la recta paralela a la dirección de afinidad que pasa por 3’.
Así obtendríamos 3.
Así obtendríamos el hexágono afín.
Tema 3: Abatimientos
Abatir un plano quiere decir girarlo sobre una línea que llamaremos charnela para apoyarlo sobre otro plano cuya lectura nos resulte más beneficiosa. Lo más común es abatir sobre el Plano de Proyección Horizontal, pero cualquier otro plano es válido.
El objetivo principal es poder leer dimensiones y ángulos en verdadera magnitud, lo cual supondrá una herramienta de gran utilidad.
Tipos de Abatimientos
Explicación de cómo abatir.
Ejercicios
Soluciones
Tema 2: Intersección de planos
La intersección entre dos planos α y β es una recta i común a ambos.
Para hallar los puntos que ambos planos tienen en común se utilizan planos auxiliares eligiéndolos preferentemente del siguiente orden:
- Los planos de proyección (pues no requiere el dibujo de ningún plano auxiliar)
- Planos paralelos a los de proyección (empleando para ello planos frontales y horizontales)
- Otro plano cualquiera


Como metodología general primero se halla la traza H2, intersección entre α2 y β2, luego V1, intersección entre α1 y β1. Uniéndolas se obtiene la recta buscada.
En la figura descriptiva anterior, halladas las trazas H2, intersección entre α2 y β2, y V1, intersección entre α1 y β1, basta con encontrar las proyecciones H1 y V2 mediante perpendiculares hasta la línea de tierra LT. Tras unir H2 y V2, H1 y V1 quedarán determinadas las proyecciones i1 y i2, proyecciones de la recta i de intersección.
TEMA 2
Ejercicios
Soluciones
Tema 1: Alfabeto del diédrico
El sistema diédrico es un método gráfico el cual consiste en obtener la imagen de un objeto (en planta y alzado), mediante la proyección de haces (rayos) proyectantes perpendiculares a dos planos principales de proyección.
plano horizontal (PH) y plano vertical (PV).
El objeto queda representado por su vista frontal (proyección en el plano vertical) y su vista superior (proyección en el plano horizontal); también se puede representar su vista lateral, como proyección auxiliar. A estas dos proyecciones se les suele llamar en el dibujo técnico Alzado y Planta. La tercera vista, la vista lateral se llamaría Perfíl.
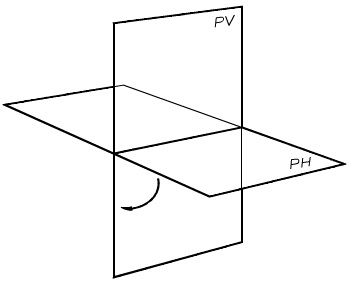
Representación de un Punto
Un punto situado en el espacio se representa mediante sus dos proyecciones (a modo de sombras) sobre los planos principales: proyección horizontal y proyección vertical.
Cota
Se denomina cota de un punto del espacio a la distancia entre él y su proyección en el plano horizontal, o lo que es lo mismo la distancia entre la proyección vertical y la línea de Tierra (LT).
Alejamiento
Se denomina alejamiento de un punto del espacio a la distancia entre el y su proyección en el plano vertical, o lo que es lo mismo a la distancia entre la proyección horizontal y la línea de Tierra (LT).
Vamos a representar un punto. Lo primero es que para dibujar sus dos proyecciones sobre los planos en un papel tendremos que abatir (abrir) los dos planos para que nos quede en dos dimensiones (las que tiene el papel) y luego dibujar sus proyecciones sobre los planos. En la figura tenemos el punto colocado en el espacio sobre los dos planos y a la derecha vemos la representación sobre el papel.

Representación de Una Recta
Una recta está definida cuando se conocen sus dos proyecciones, horizontal y vertical. La proyección de una recta sobre un plano es otra recta, formada por la proyección de todos los puntos de ella. Conociendo las parejas de proyecciones (sobre el plano vertical y sobre el horizontal) de dos puntos de una recta, se obtiene la proyección uniendo los dos puntos. Fíjate en la figura hemos cogido dos puntos cualquiera de la recta A y B para sacar sus proyecciones. En la parte de abajo sería como se dibujaría en el papel la recta, mediante sus proyecciones.
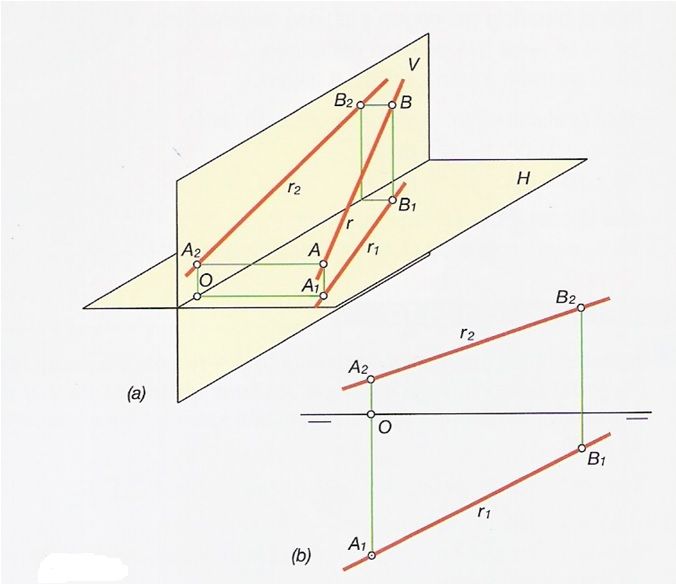
Veamos como sería una recta paralela a los dos planos:
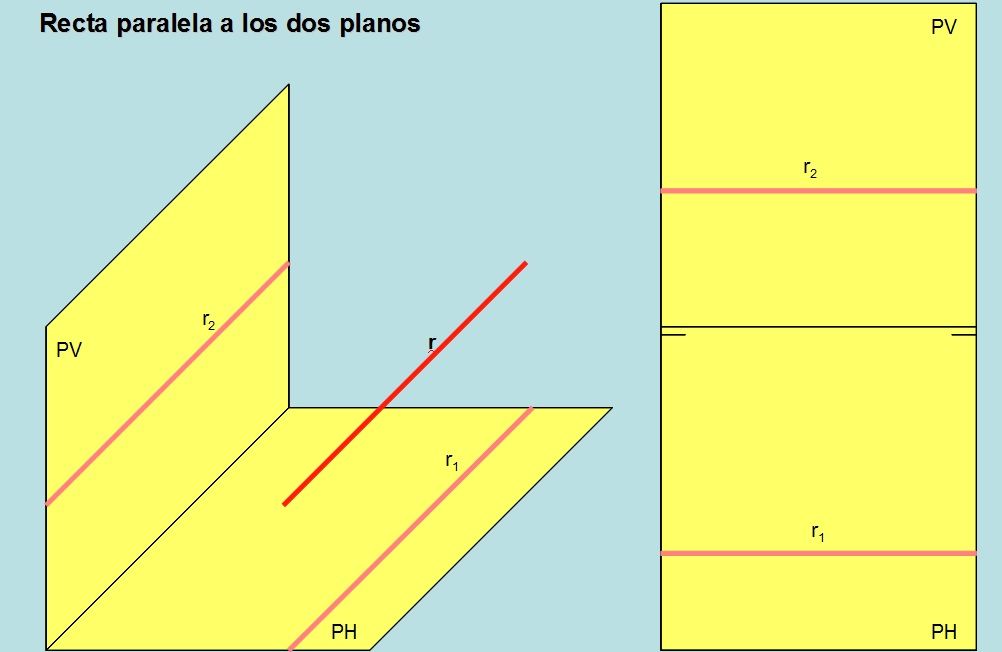
Ahora veamos dos rectas en diferentes posiciones y su representaciones:
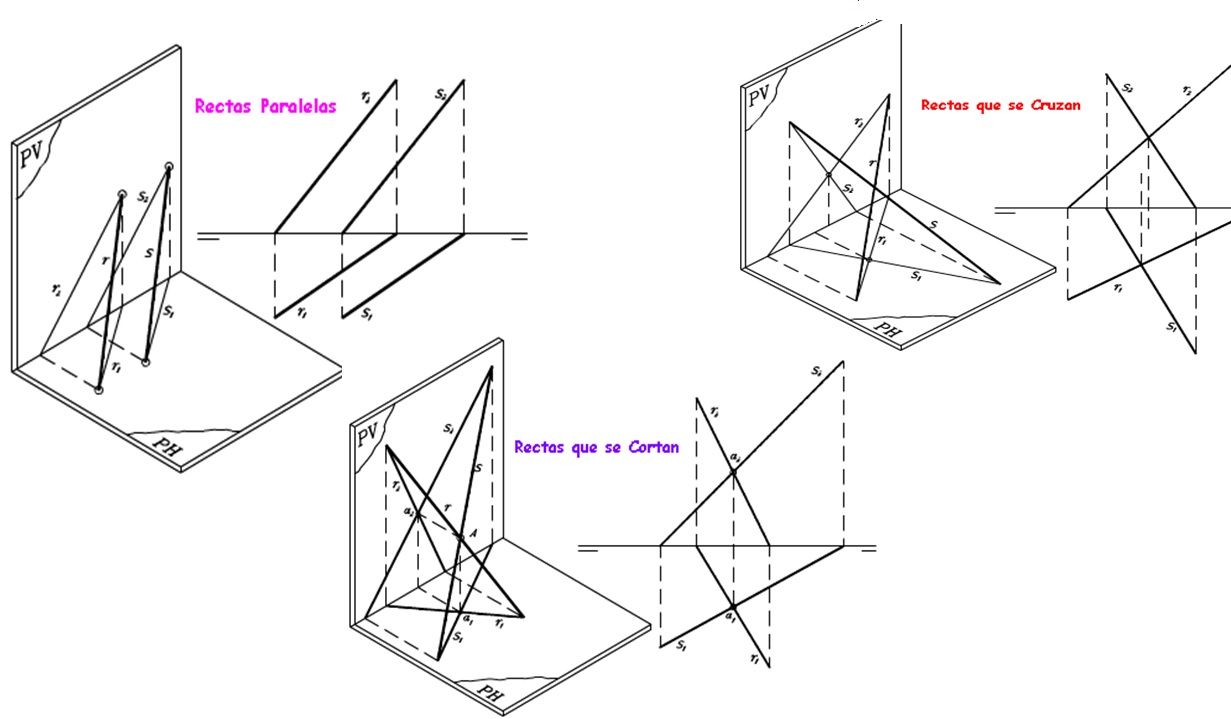
Representación de Un Plano
Hasta ahora hemos aprendido los conceptos y procedimientos para determinar las proyecciones diédricas de un punto y una recta; y aunque hemos nombrado algunas veces al plano, solamente ha sido para referirnos a los de proyección.
Generalmente entendemos que una superficie plana es aquella que puede contener una recta imaginaria en cualquier dirección.
La definición anterior la podemos aplicar a la hora de referirnos a un plano en el sistema diédrico.
Así pues, las caras de una forma, objeto, poliedro, etc., son planos delimitados por aristas (rectas) y vértices (puntos).
En el sistema diédrico entendemos que un plano es una superficie plana infinita e ilimitada.
Para definir un plano necesitamos los siguientes elementos geométricos: tres puntos cualesquiera que no estén alineados, una recta y un punto exterior a ella, dos rectas que se cortan y dos rectas paralelas.
Un plano se representa mediante sus trazas. Las Trazas de un plano son las rectas intersección del plano con los planos de proyección.
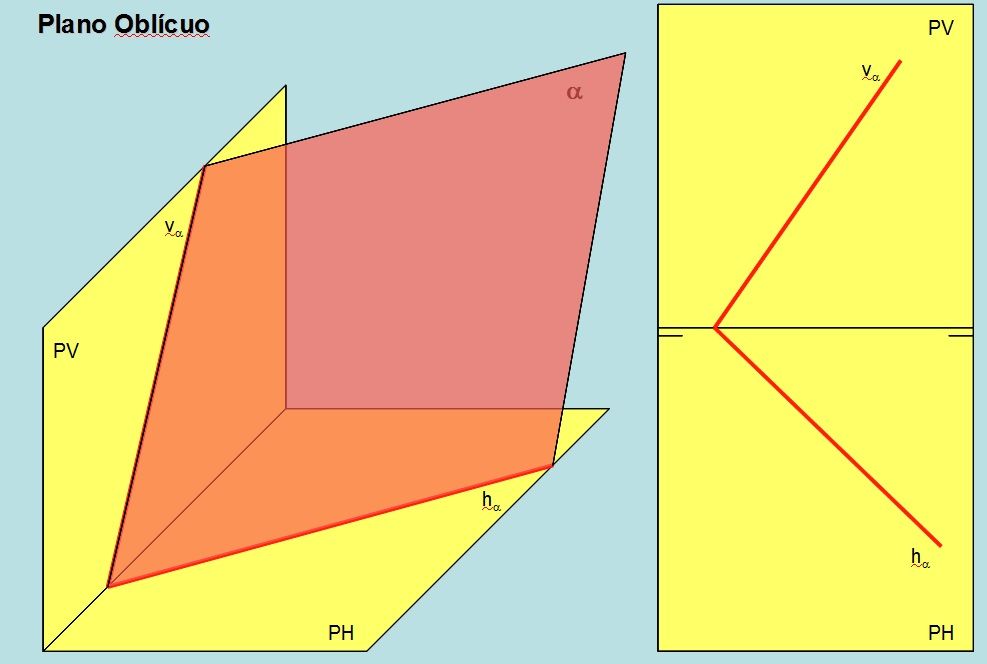
Veamos situaciones de planos en sistema diedrico diferentes.
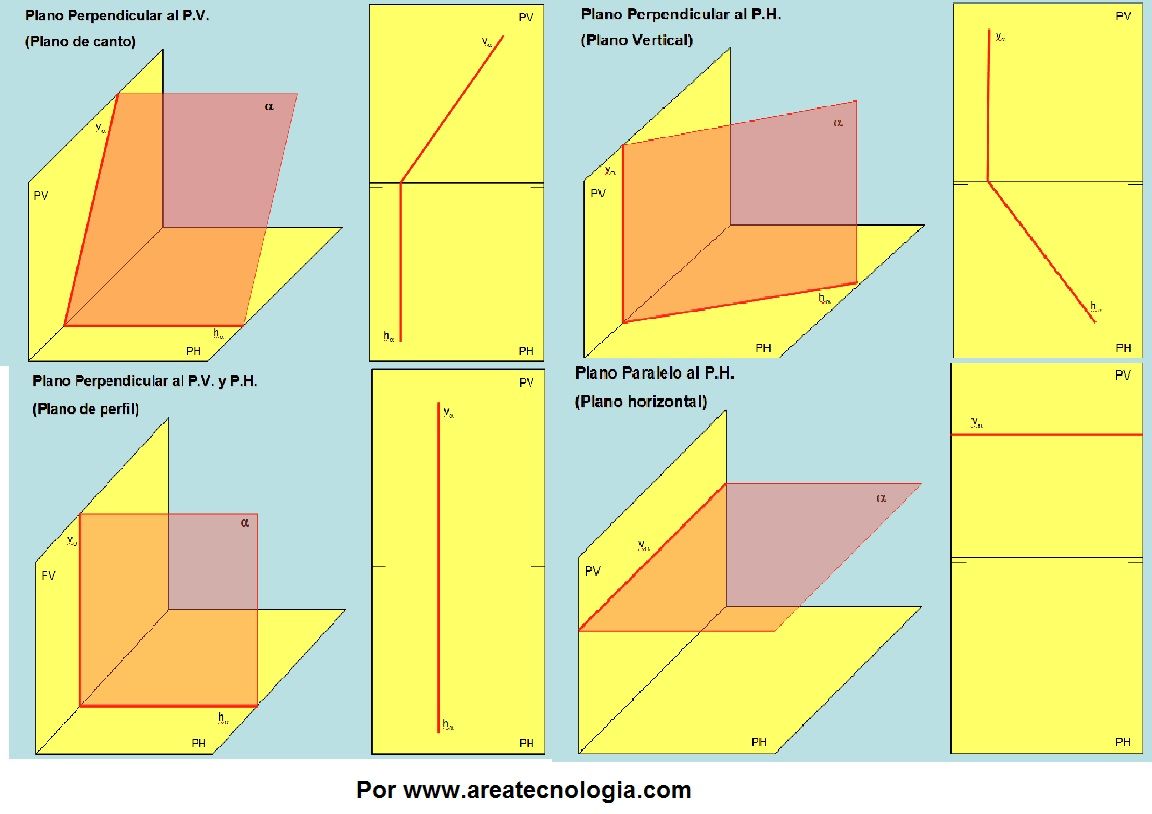
En la siguiente presentación os dejamos más sobre diedrico con ejercicios resueltos para que veas como se representan más rectas y planos en diedrico.
plano horizontal (PH) y plano vertical (PV).
El objeto queda representado por su vista frontal (proyección en el plano vertical) y su vista superior (proyección en el plano horizontal); también se puede representar su vista lateral, como proyección auxiliar. A estas dos proyecciones se les suele llamar en el dibujo técnico Alzado y Planta. La tercera vista, la vista lateral se llamaría Perfíl.

Representación de un Punto
Un punto situado en el espacio se representa mediante sus dos proyecciones (a modo de sombras) sobre los planos principales: proyección horizontal y proyección vertical.
Cota
Se denomina cota de un punto del espacio a la distancia entre él y su proyección en el plano horizontal, o lo que es lo mismo la distancia entre la proyección vertical y la línea de Tierra (LT).
Alejamiento
Se denomina alejamiento de un punto del espacio a la distancia entre el y su proyección en el plano vertical, o lo que es lo mismo a la distancia entre la proyección horizontal y la línea de Tierra (LT).
Vamos a representar un punto. Lo primero es que para dibujar sus dos proyecciones sobre los planos en un papel tendremos que abatir (abrir) los dos planos para que nos quede en dos dimensiones (las que tiene el papel) y luego dibujar sus proyecciones sobre los planos. En la figura tenemos el punto colocado en el espacio sobre los dos planos y a la derecha vemos la representación sobre el papel.

Representación de Una Recta
Una recta está definida cuando se conocen sus dos proyecciones, horizontal y vertical. La proyección de una recta sobre un plano es otra recta, formada por la proyección de todos los puntos de ella. Conociendo las parejas de proyecciones (sobre el plano vertical y sobre el horizontal) de dos puntos de una recta, se obtiene la proyección uniendo los dos puntos. Fíjate en la figura hemos cogido dos puntos cualquiera de la recta A y B para sacar sus proyecciones. En la parte de abajo sería como se dibujaría en el papel la recta, mediante sus proyecciones.

Veamos como sería una recta paralela a los dos planos:

Ahora veamos dos rectas en diferentes posiciones y su representaciones:

Representación de Un Plano
Hasta ahora hemos aprendido los conceptos y procedimientos para determinar las proyecciones diédricas de un punto y una recta; y aunque hemos nombrado algunas veces al plano, solamente ha sido para referirnos a los de proyección.
Generalmente entendemos que una superficie plana es aquella que puede contener una recta imaginaria en cualquier dirección.
La definición anterior la podemos aplicar a la hora de referirnos a un plano en el sistema diédrico.
Así pues, las caras de una forma, objeto, poliedro, etc., son planos delimitados por aristas (rectas) y vértices (puntos).
En el sistema diédrico entendemos que un plano es una superficie plana infinita e ilimitada.
Para definir un plano necesitamos los siguientes elementos geométricos: tres puntos cualesquiera que no estén alineados, una recta y un punto exterior a ella, dos rectas que se cortan y dos rectas paralelas.
Un plano se representa mediante sus trazas. Las Trazas de un plano son las rectas intersección del plano con los planos de proyección.

Veamos situaciones de planos en sistema diedrico diferentes.

En la siguiente presentación os dejamos más sobre diedrico con ejercicios resueltos para que veas como se representan más rectas y planos en diedrico.










No hay comentarios:
Publicar un comentario